Transformations to Normality

Author

Christofer Rodriguez & Said Salehe

Published

May 23, 2023

Transforming Data

Introduction

Most parametric tests require that residuals be normally distributed and have equal variance among other assumptions. However, in practice, most data does not fit these assumptions. One approach to dealing with data that violate normality assumption is to transform data (one or more variables) to better follow a normal distribution. In most cases, the dependent variable needs to be transformed however, in complex models and multiples regression, both dependent and independent variables that deviate greatly from normal are transformed.

There is nothing illicit in transforming variables, but care must be exercised on how the results from analyses with transformed variables are reported. For example, when comparing the difference between groups using log-transformed data you would want to present the mean difference. To present means or other summary statistics, you might present the mean of transformed values or back transform means to their original units. Some measurements in nature are naturally normally distributed and does not require prior transformation before analysis. Other measurements are naturally log-normally distributed. These include some natural pollutants in water or air and metabolites in biological systems. In these cases there many low values with fewer high values and even fewer very high values.

Skewness and Common Transformation

Skewness is the measure of symmetry or, more precisely, the lack of symmetry. A distribution or data set is symmetric if the left and right of the centre point look more or less the same.

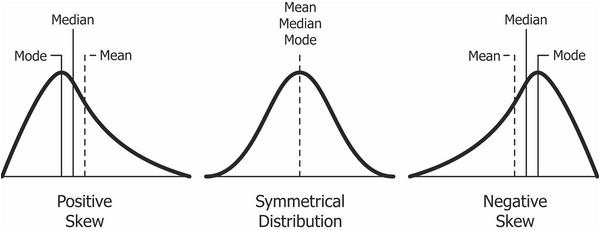
**Adopted From: Clojure Data Science by Henry Garner**

Distribution can be normal, right-skewed (positive skew) or left-skewed (negative skew). For right-skewed data, the tail is on the right, while For left-skewed data the tail is on the left.

common transformation methods include

square root, cube root, and log - For right-skewed data.
square root (constant – x), cube root (constant – x), and log (constant – x) - For left-skewed data.

Another approach is to use a general power transformation, such as Tukey’s Ladder of Powers or a Box-Cox transformation. These methods determine a lambda value, which is used as the power coefficient to transform values. X.new = X ^ lambda for Tukey, and X.new = (X ^ lambda - 1) / lambda for Box-Cox.

Assumptions

Hypothesis - The metobolite data do not meet the assumptions of normality.

Installing Necessary Packages

To perform a transformation to normality, we need a couple of packages - Some are necessary, and others are preference. We need tidyverse() for reading, wrangling, and visualizing data. We also used ggpubr() for customized visualization of skewness.

Package descriptions

ggpubr: ggpubr provides some easy-to-use functions for creating and customizing ‘ggplot2’- based publication ready plots (requires ggplot2)
psych- Procedures for Psychological, Psychometric, and Personality Research: A general purpose toolbox developed originally for personality, psychometric theory and experimental psychology.
tidyverse: The ‘tidyverse’ is a set of packages that work in harmony because they share common data representations and ‘API’ design.

Code

# First we must install or load the necessary packages
# install.packages("ggpubr") 
# install.packages("psych") 
# install.packages("tidyverse") 

library(ggpubr) 
library(psych) 
library(tidyverse) 
library(skimr)
library(gtsummary)

Reading Metabolites Data

As mentioned in the introduction above, some data are naturally log-normally distributed. to demonstrate the transformation of skewed data back to normal, we used a data set that is commonly known to be right skewed. The data set contains urinary metabolites used to predict skeletal muscle wasting associated with cancer. The data can be downloaded from the MetaboAnalyst web page under one-factor statistical examples [data set download]. The original article that published the data can be found Here. Read the data using the read_csv() function.

Code

# Importing the data set from our local drive. 
Meta <- 
  read_csv("/Users/christoferrodriguez/R_Statistical_Folder/PHC_6099/PHC6900/human_cachexia.csv",
           col_names = TRUE) # Using the column names already assigned in the file. 
# We are assigning the data set a name of `Meta` to start so we can explore the 
#   data.

Code

# Display the first 6 rows of the data set
head(Meta) # This shows that there is a lot of columns; we only need three.

# A tibble: 6 × 65
  `Patient ID` `Muscle loss` `1,6-Anhydro-beta-D-glucose` `1-Methylnicotinamide`
  <chr>        <chr>                                <dbl>                  <dbl>
1 PIF_178      cachexic                              40.8                   65.4
2 PIF_087      cachexic                              62.2                  340. 
3 PIF_090      cachexic                             270.                    64.7
4 NETL_005_V1  cachexic                             154.                    53.0
5 PIF_115      cachexic                              22.2                   73.7
6 PIF_110      cachexic                             213.                    31.8
# ℹ 61 more variables: `2-Aminobutyrate` <dbl>, `2-Hydroxyisobutyrate` <dbl>,
#   `2-Oxoglutarate` <dbl>, `3-Aminoisobutyrate` <dbl>,
#   `3-Hydroxybutyrate` <dbl>, `3-Hydroxyisovalerate` <dbl>,
#   `3-Indoxylsulfate` <dbl>, `4-Hydroxyphenylacetate` <dbl>, Acetate <dbl>,
#   Acetone <dbl>, Adipate <dbl>, Alanine <dbl>, Asparagine <dbl>,
#   Betaine <dbl>, Carnitine <dbl>, Citrate <dbl>, Creatine <dbl>,
#   Creatinine <dbl>, Dimethylamine <dbl>, Ethanolamine <dbl>, Formate <dbl>, …

Variables of Interest

We are going to look at the following metabolite variables:

Citrate
Creatine
Creatinine

Citrate is involved in both energy production and removal of toxic ammonia. High or Low levels of Citrate can indicate various medical indications that need additional testing. One example of an indication is liver and kidney functioning.

Creatine is an amino acid located mostly in your body’s muscles as well as in the brain. Most people get creatine through seafood and red meat — though at levels far below those found in synthetically made creatine supplements. The body’s liver, pancreas and kidneys also can make about 1 gram of creatine per day.

Creatinine is a chemical waste product of Creatine, which comes from the normal wear and tear of the muscles in the body. Creatinine is filtered out by the kidneys. This test is done to identify the kidney function.

Because we only need these three variables, we will select only the first two columns, plus these three columns and create a new dataset to use in our analysis.

Code

#Create a new data set to use with only our selected columns.
Meta_df <- 
  Meta %>% 
  select(
    `Patient ID`, 
    `Muscle loss`,
    Citrate,
    Creatine, 
    Creatinine
  )

# View the first 6 rows of the new data set.
head(Meta_df)

# A tibble: 6 × 5
  `Patient ID` `Muscle loss` Citrate Creatine Creatinine
  <chr>        <chr>           <dbl>    <dbl>      <dbl>
1 PIF_178      cachexic        3714.    196.      16482.
2 PIF_087      cachexic        2618.    213.      15835.
3 PIF_090      cachexic         863.    221.      24588.
4 NETL_005_V1  cachexic       13630.     85.6     20952.
5 PIF_115      cachexic         854.    106.       6768.
6 PIF_110      cachexic        1959.    200.      15678.

We are going to explore the data using the describe() function in the psych package. This will provide us with the following information:

Variables
Mean
Standard Deviation (SD)
Median
Minimum
Maximum
Range
Skew
Kurtosis
Standard Error (SE)

Code

# We are going to explore the data by summarizing the data using the describe function in the psych package.
describe(Meta_df)

             vars  n    mean      sd  median trimmed     mad     min      max
Patient ID*     1 77   39.00   22.37   39.00   39.00   28.17    1.00    77.00
Muscle loss*    2 77    1.39    0.49    1.00    1.37    0.00    1.00     2.00
Citrate         3 77 2235.35 2166.57 1790.05 1928.24 1687.32   59.74 13629.61
Creatine        4 77  126.83  273.22   44.26   71.83   53.88    2.75  1863.11
Creatinine      5 77 8733.97 6477.62 7631.20 7994.69 6621.16 1002.25 33860.35
                range skew kurtosis     se
Patient ID*     76.00 0.00    -1.25   2.55
Muscle loss*     1.00 0.44    -1.83   0.06
Citrate      13569.87 2.43     9.00 246.90
Creatine      1860.36 4.84    25.42  31.14
Creatinine   32858.10 1.15     1.64 738.19

Check For Normality

Using the selected metabolites, plot histograms to check for the distribution of specific metabolites. Creatinine, Creatine and Citrate are used as examples but other metabolites can be used. These three metabolites are right skewed (positively skewed).

Code

# Next we will create a histogram to view the data as it currently is. 
hist(Meta_df$Citrate,
     main = "Histogram of Citrate",
     xlab = "Citrate")

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Citrate) +
  labs(title = "Citrate levels QQ-plot") +
  stat_qq() + stat_qq_line()

Code

hist(Meta_df$Creatine,
     main = "Histogram of Creatine",
     xlab = "Creatine")

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Creatine) +
  labs(title = "Creatine levels QQ-plot") +
  stat_qq() + stat_qq_line()

Code

hist(Meta_df$Creatinine,
     main = "Histogram of Creatinine",
     xlab = "Creatinine")

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Creatinine) +
  labs(title = "Creatinine levels QQ-plot") +
  stat_qq() + stat_qq_line()

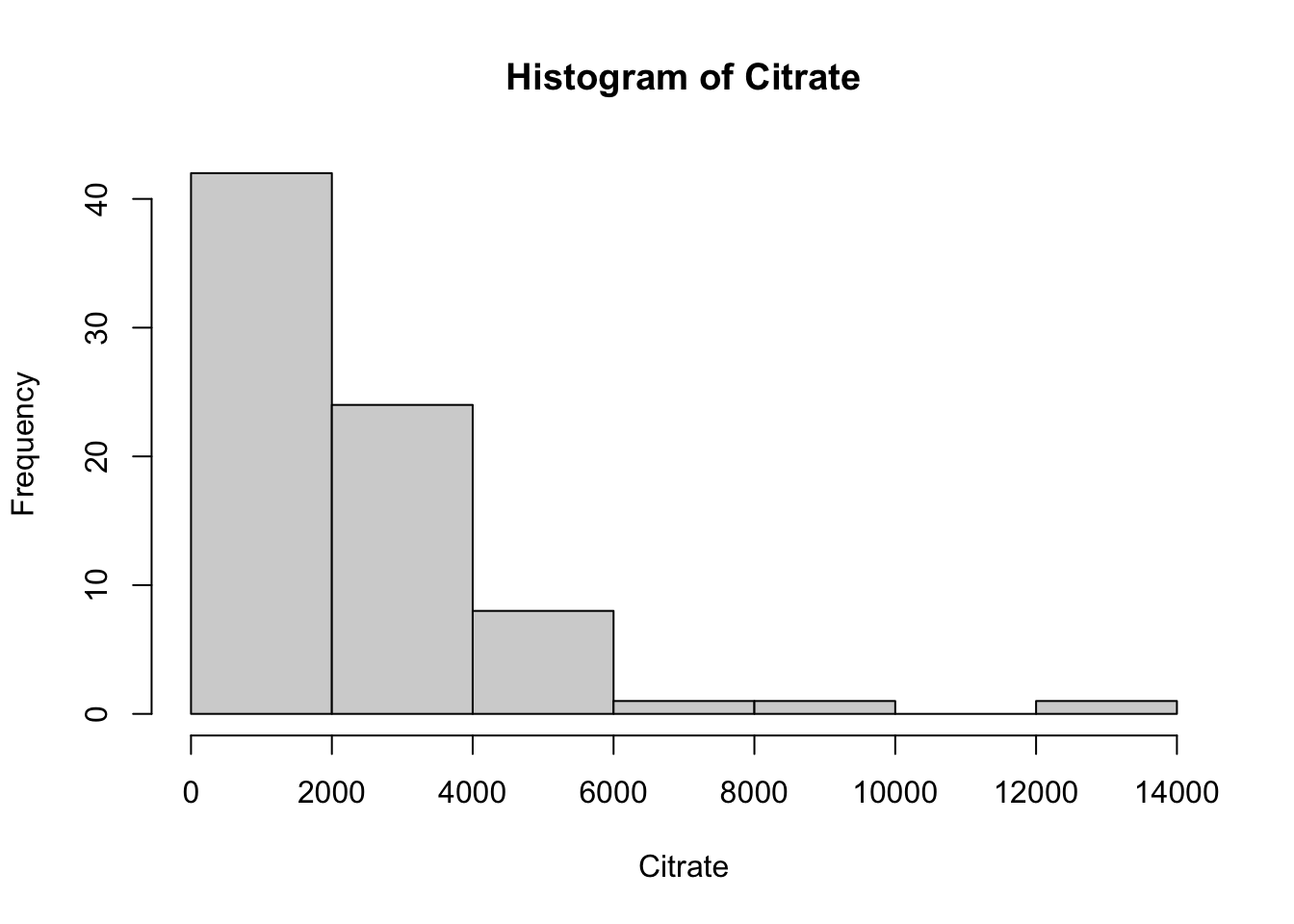
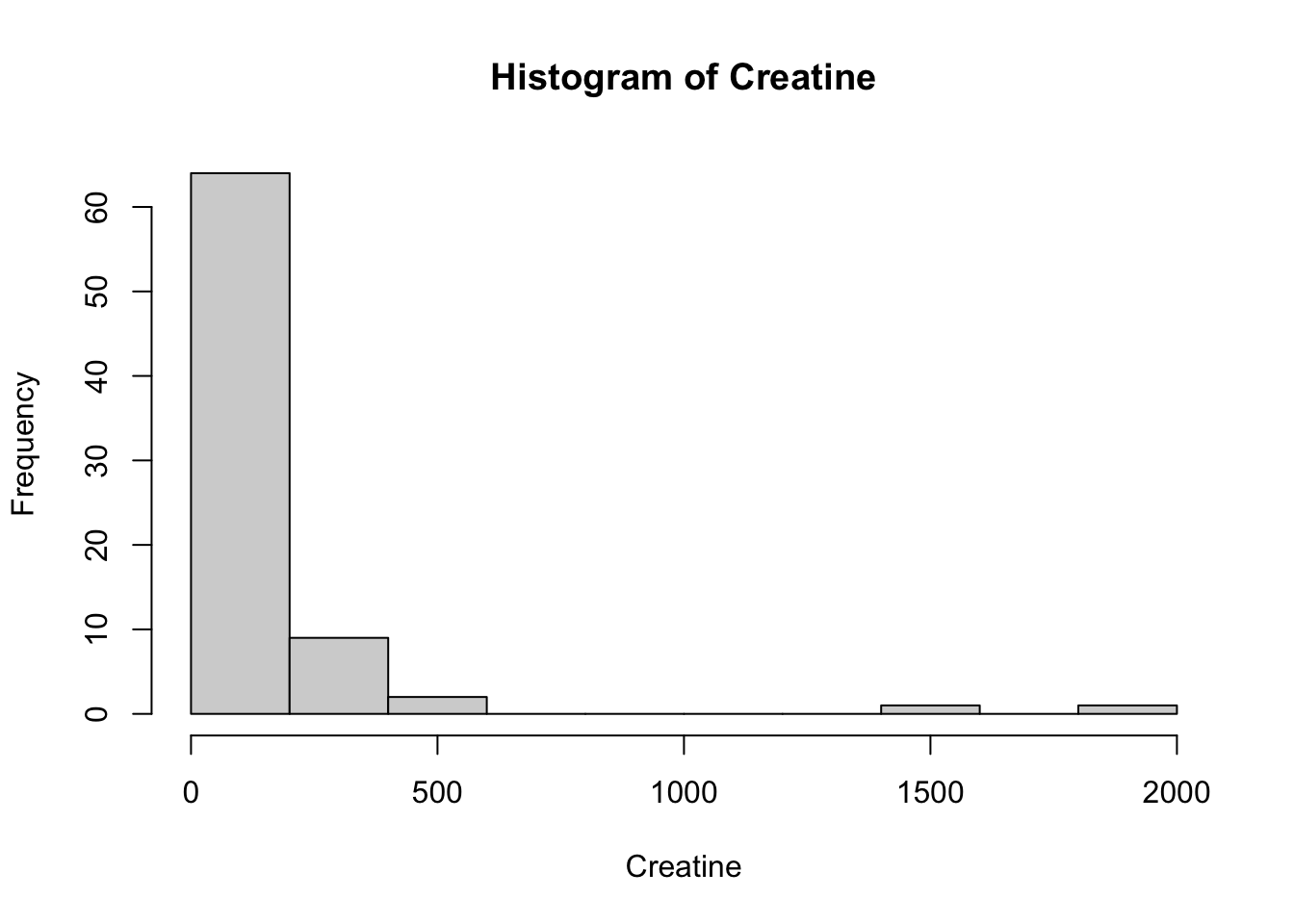
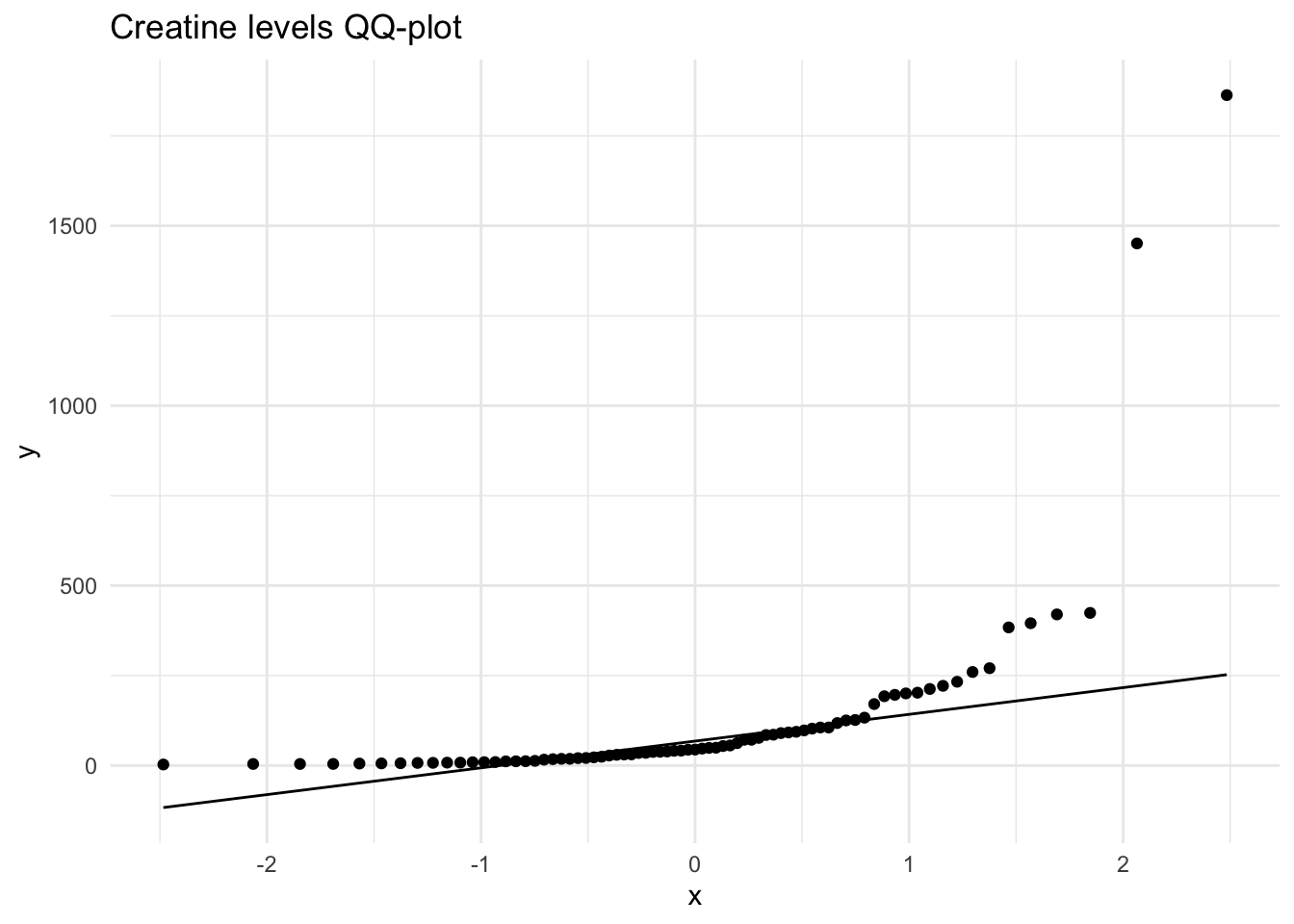
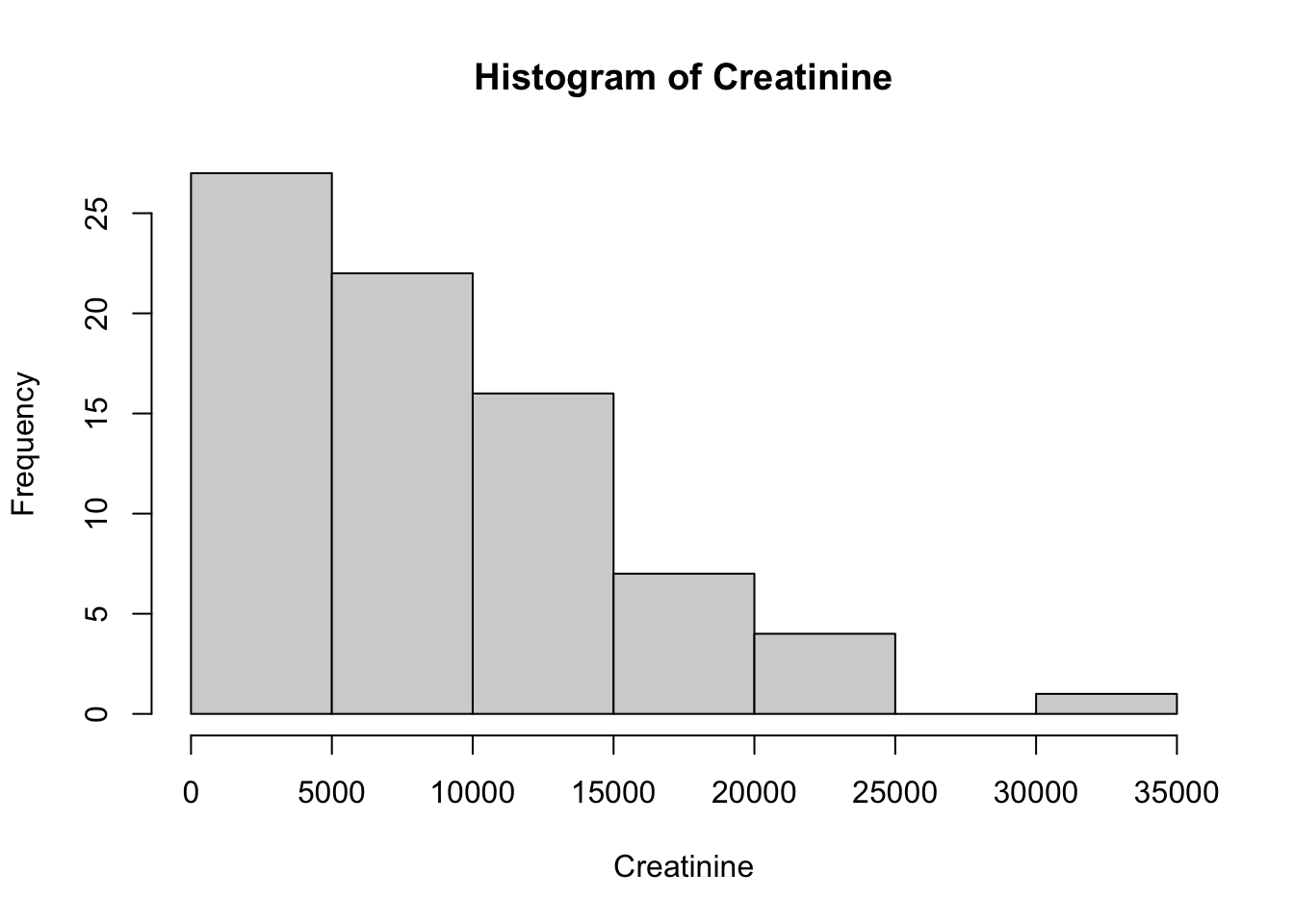
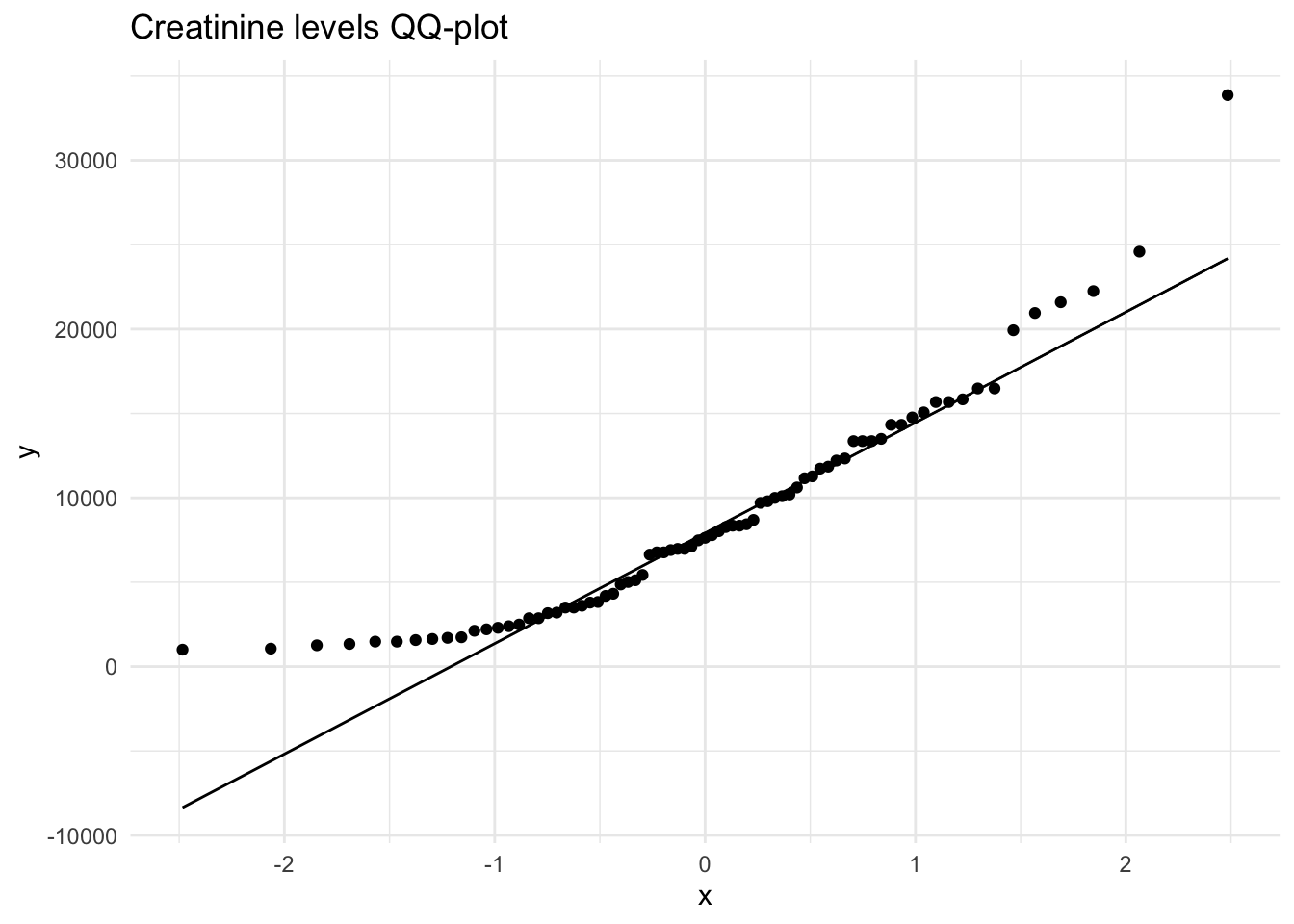
Next, we will create a distribution plot of the current variables to see how it looks compared to a normal distribution plot. To do this, we will use the ggpubr package that will allow us to enhance the ggplot functions available in the tidyverse package. The function we will use is ggdensity.

Code

# Plot the distribution of the Citrate variable
ggdensity(Meta_df$Citrate, fill = "lightgray", title = "Distribution plot of Citrate") +
  scale_x_continuous() +
  xlab("Citrate Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Plot the distribution of the Creatine variable
ggdensity(Meta_df$Creatine, fill = "lightgray", title = "Distribution plot of Creatine") +
  scale_x_continuous() +
  xlab("Creatine Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Plot the distribution of the Creatinine variable
ggdensity(Meta_df$Creatinine, fill = "lightgray", title = "Distribution plot of Creatinine") +
  scale_x_continuous() +
  xlab("Creatinine Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

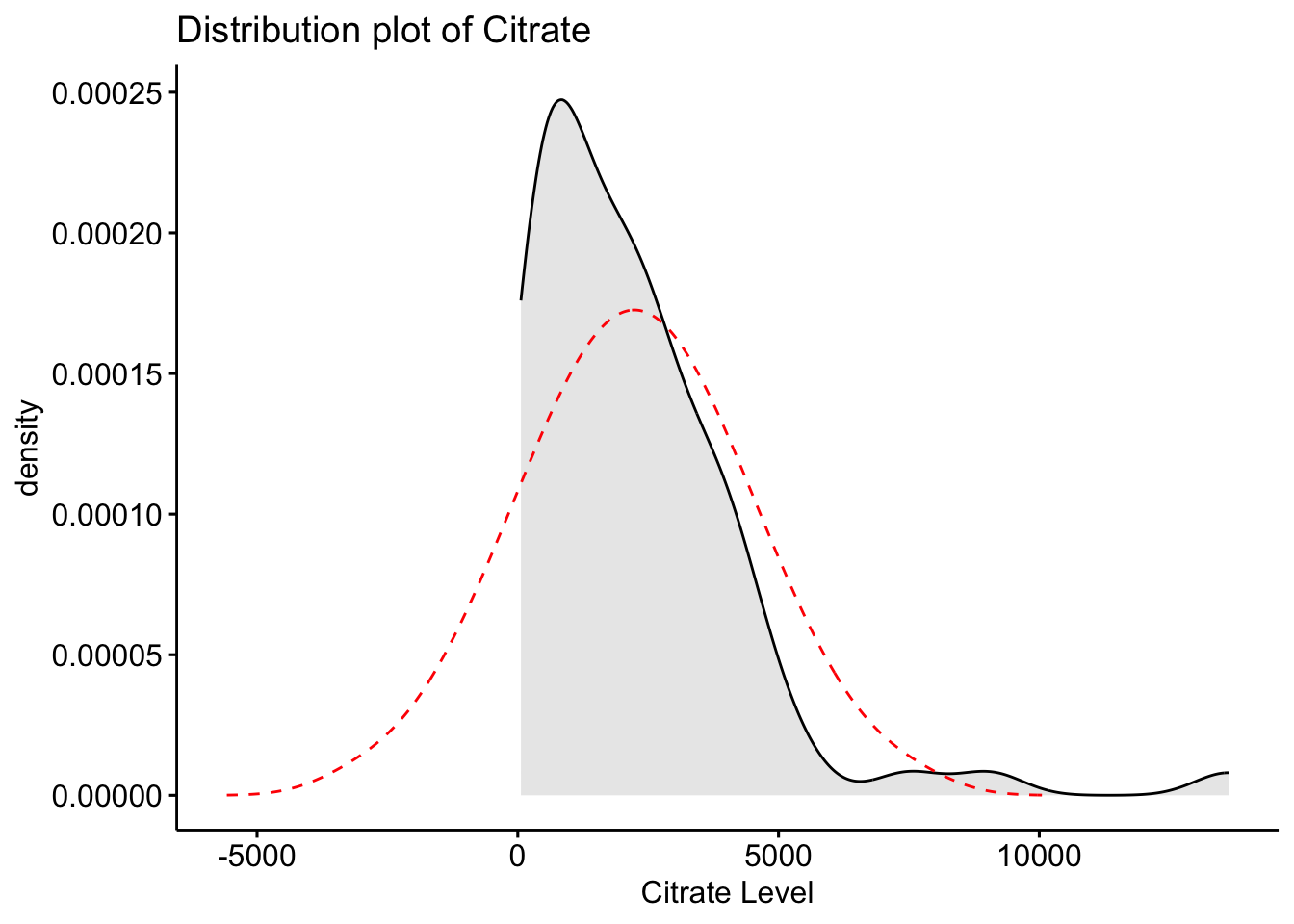
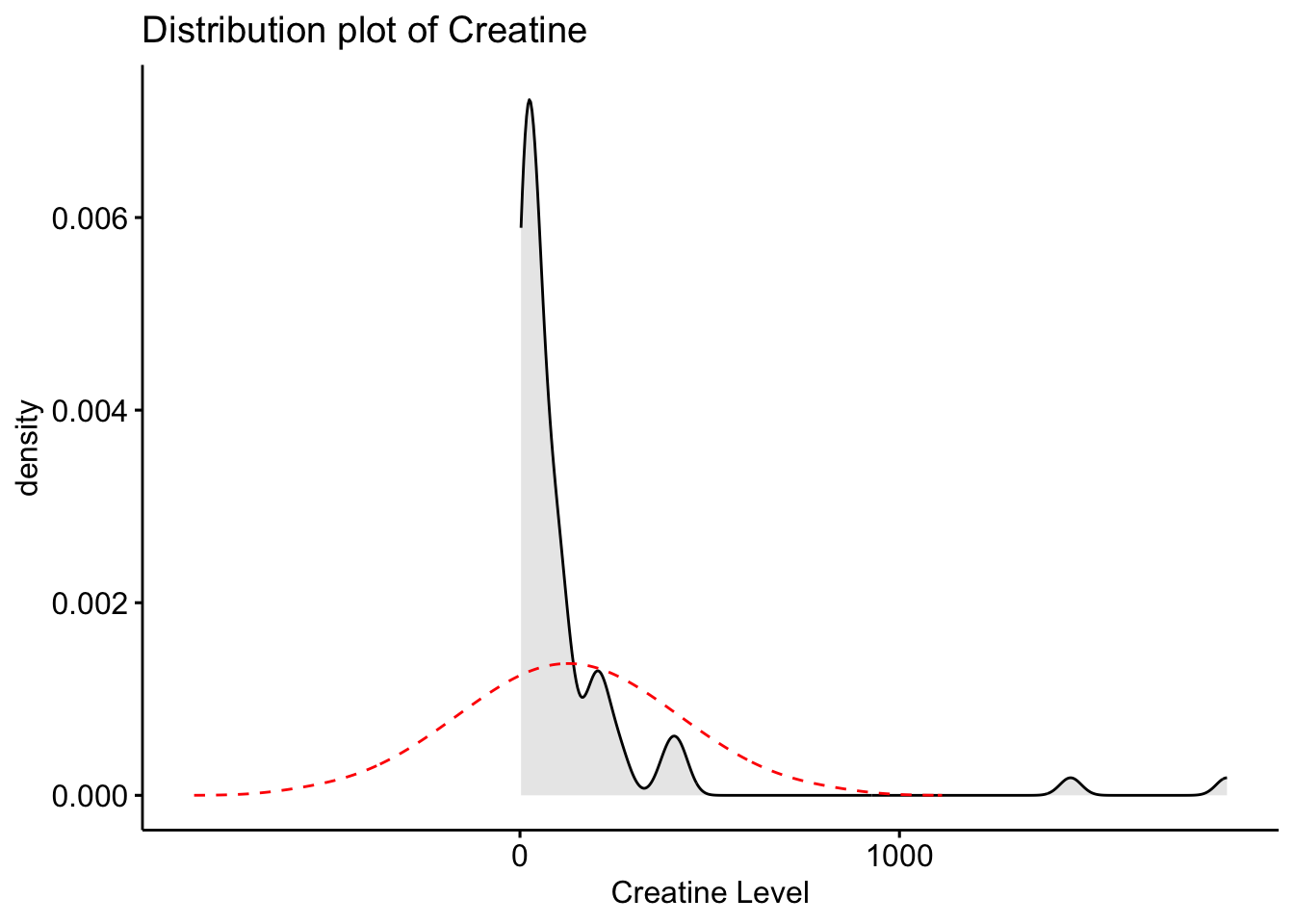
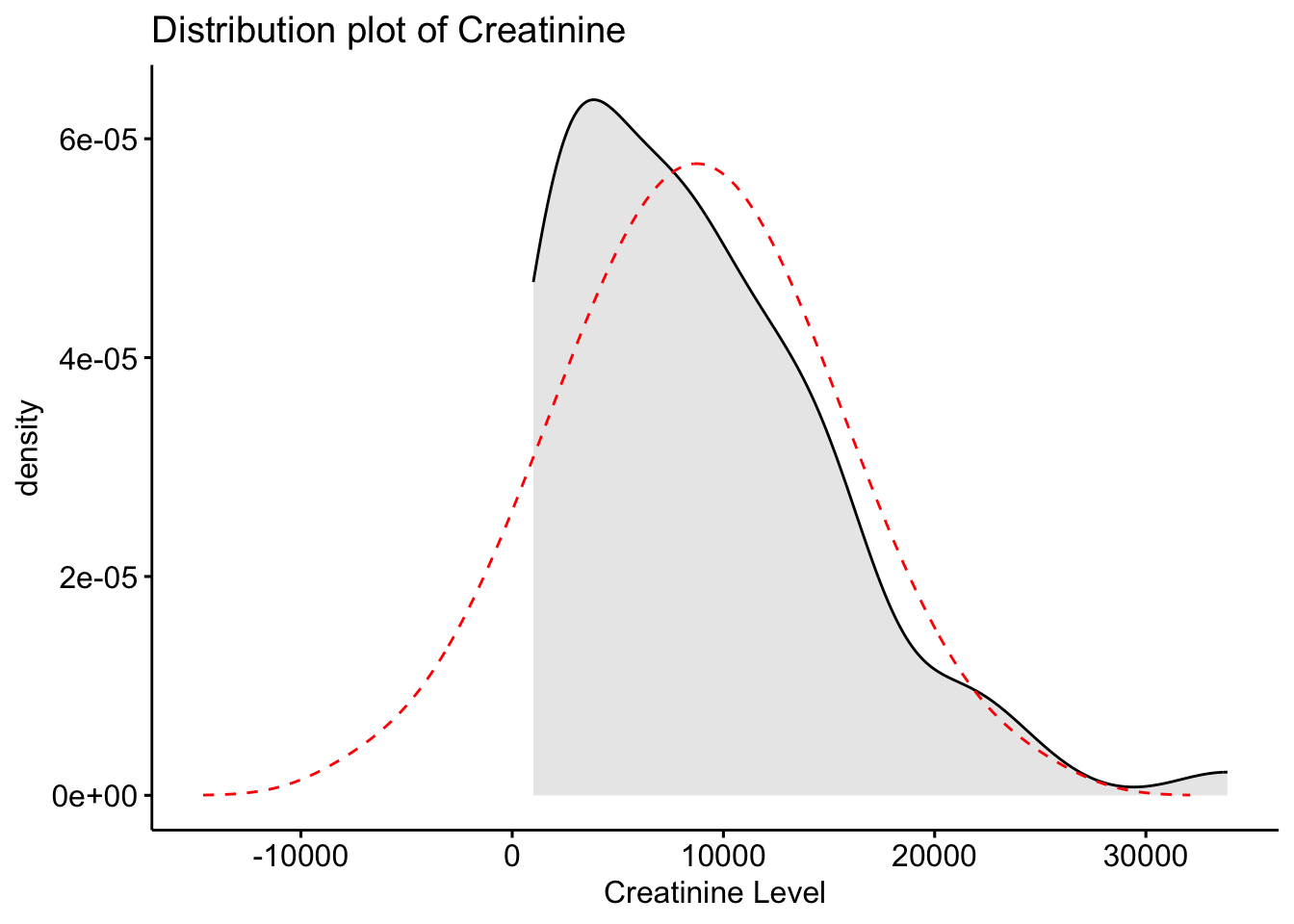
Here we can see that our original variables to not fit the normal distribution, and therefore would need to be transformed.

Transforming Right Skewed Data

Now that we see that these variables do not follow the normal distribution, we can identify what type of distribution they are, and what transformation might work best for these variables. To transform right skewed metabolites data, we used square root and log transformation.

Root Transformation

Code

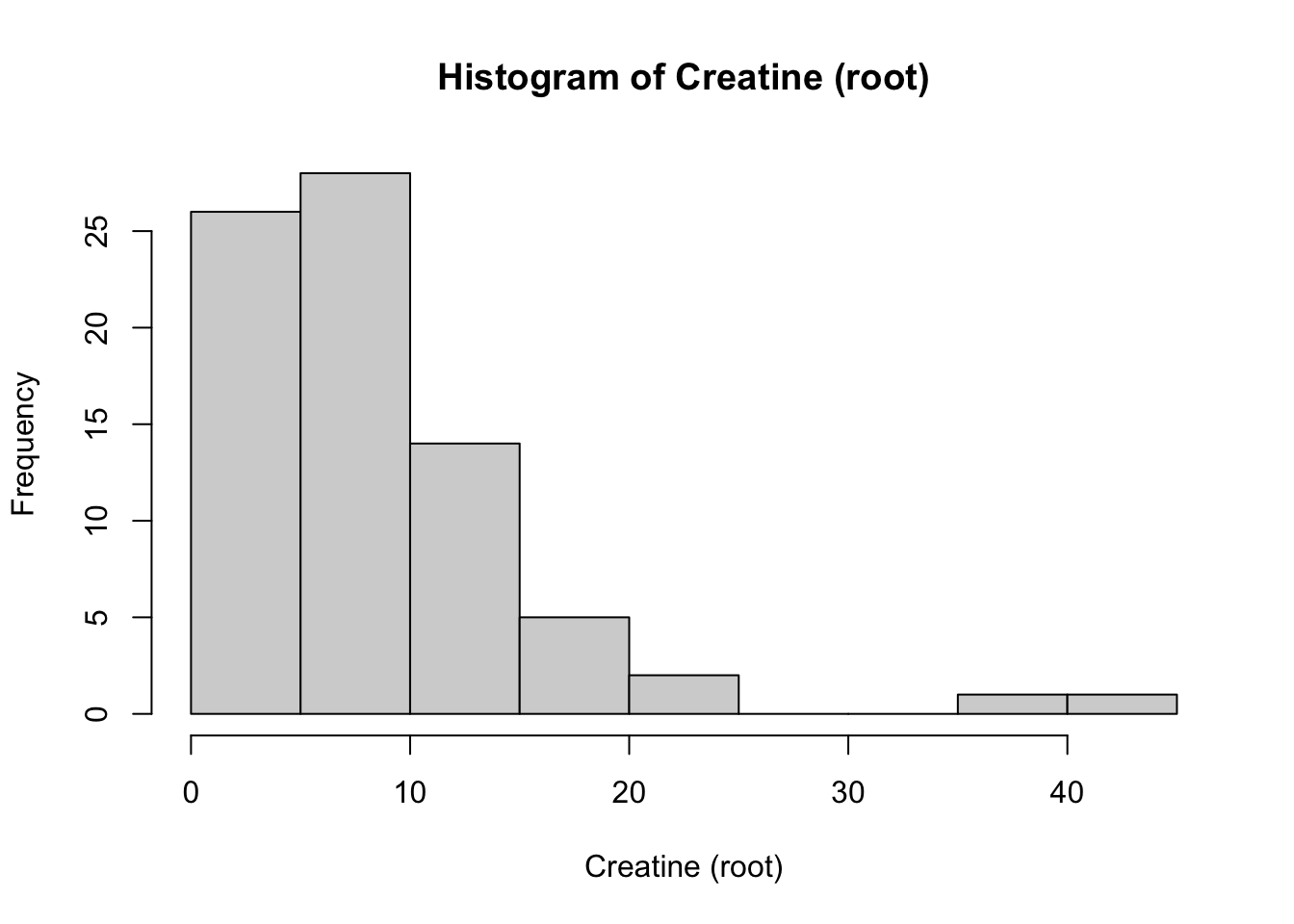
# Transforming the original variable into a new rooted variable.
Meta_df$Citrate_root <- sqrt(Meta_df$Citrate)
Meta_df$Creatine_root <- sqrt(Meta_df$Creatine)
Meta_df$Creatinine_root <- sqrt(Meta_df$Creatinine)

# Creating a histogram of the new rooted variables.
hist(Meta_df$Citrate_root,
     main = "Histogram of Citrate (root)",
     xlab = "Citrate (root)")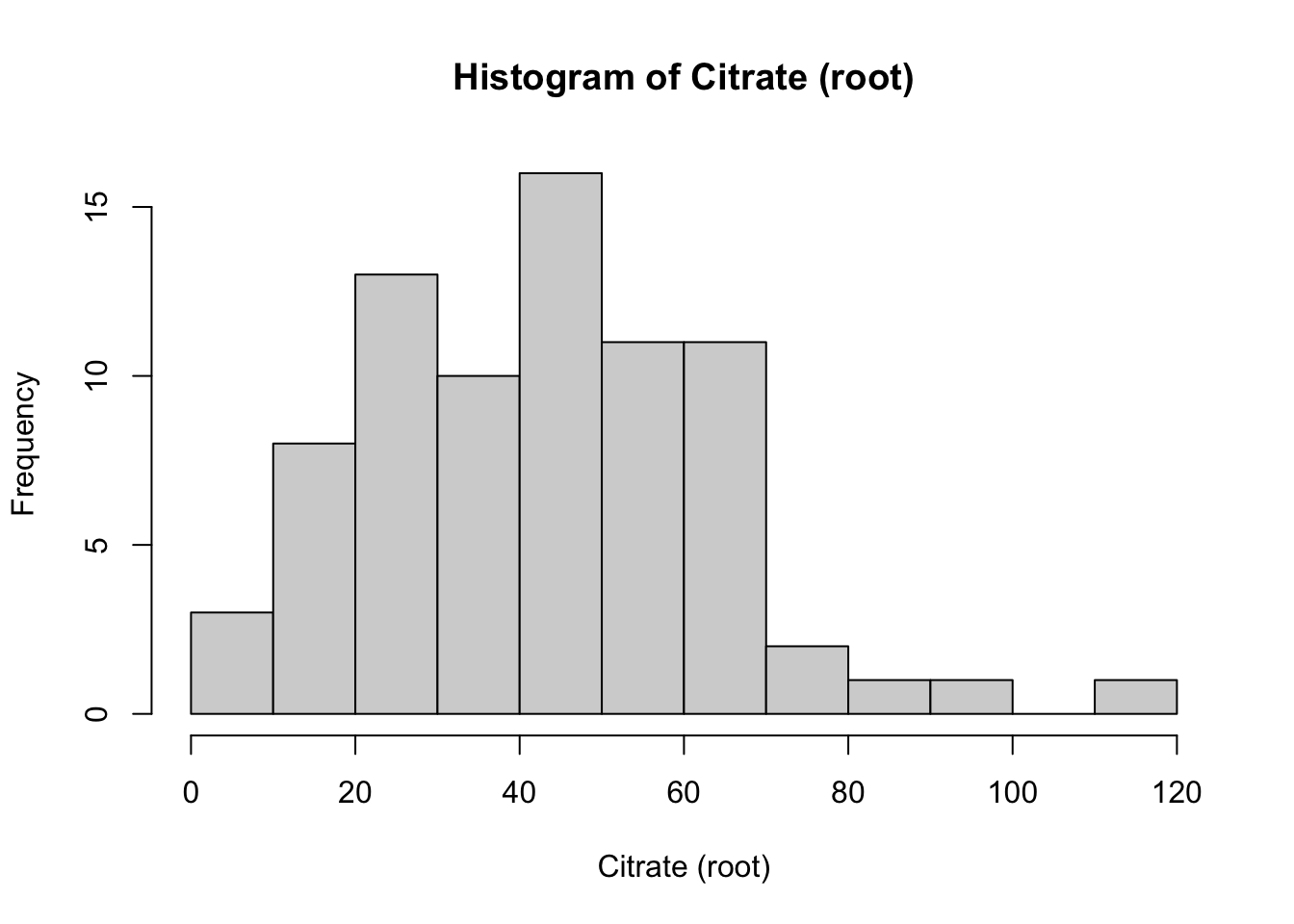

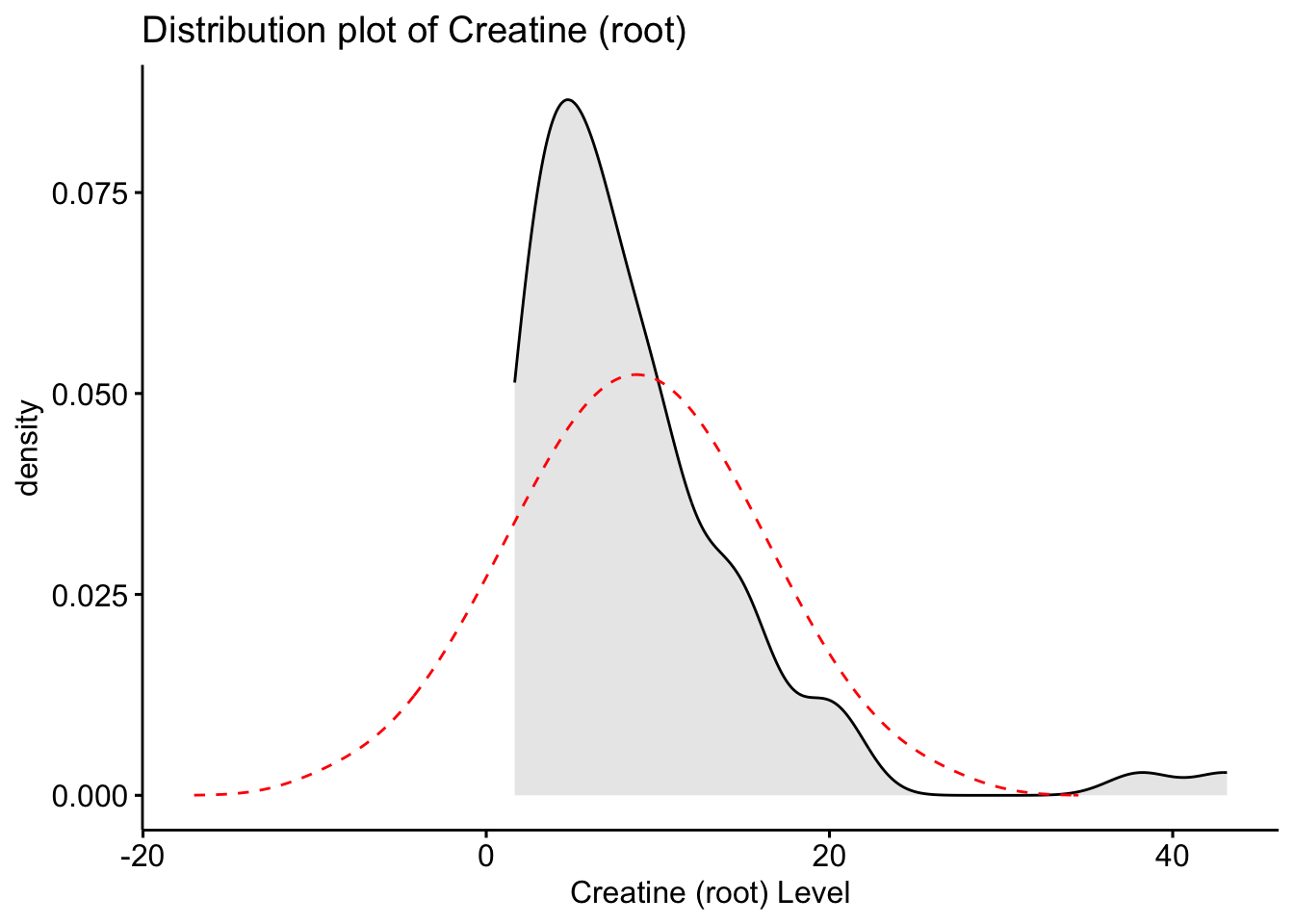
Code

hist(Meta_df$Creatine_root,
     main = "Histogram of Creatine (root)",
     xlab = "Creatine (root)")

Code

hist(Meta_df$Creatinine_root,
     main = "Histogram of Creatinine (root)",
     xlab = "Creatinine (root)")

Code

# Create a plot of the distribution of the new rooted variable Citrate
ggdensity(Meta_df$Citrate_root, fill = "lightgray", title = "Distribution plot of Citrate (root)") +
  scale_x_continuous() +
  xlab("Citrate (root) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Create a plot of the distribution of the new rooted variable Creatine
ggdensity(Meta_df$Creatine_root, fill = "lightgray", title = "Distribution plot of Creatine (root)") +
  scale_x_continuous() +
  xlab("Creatine (root) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Create a plot of the distribution of the new rooted variable Creatinine
ggdensity(Meta_df$Creatinine_root, fill = "lightgray", title = "Distribution plot of Creatinine (root)") +
  scale_x_continuous() +
  xlab("Creatinine (root) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")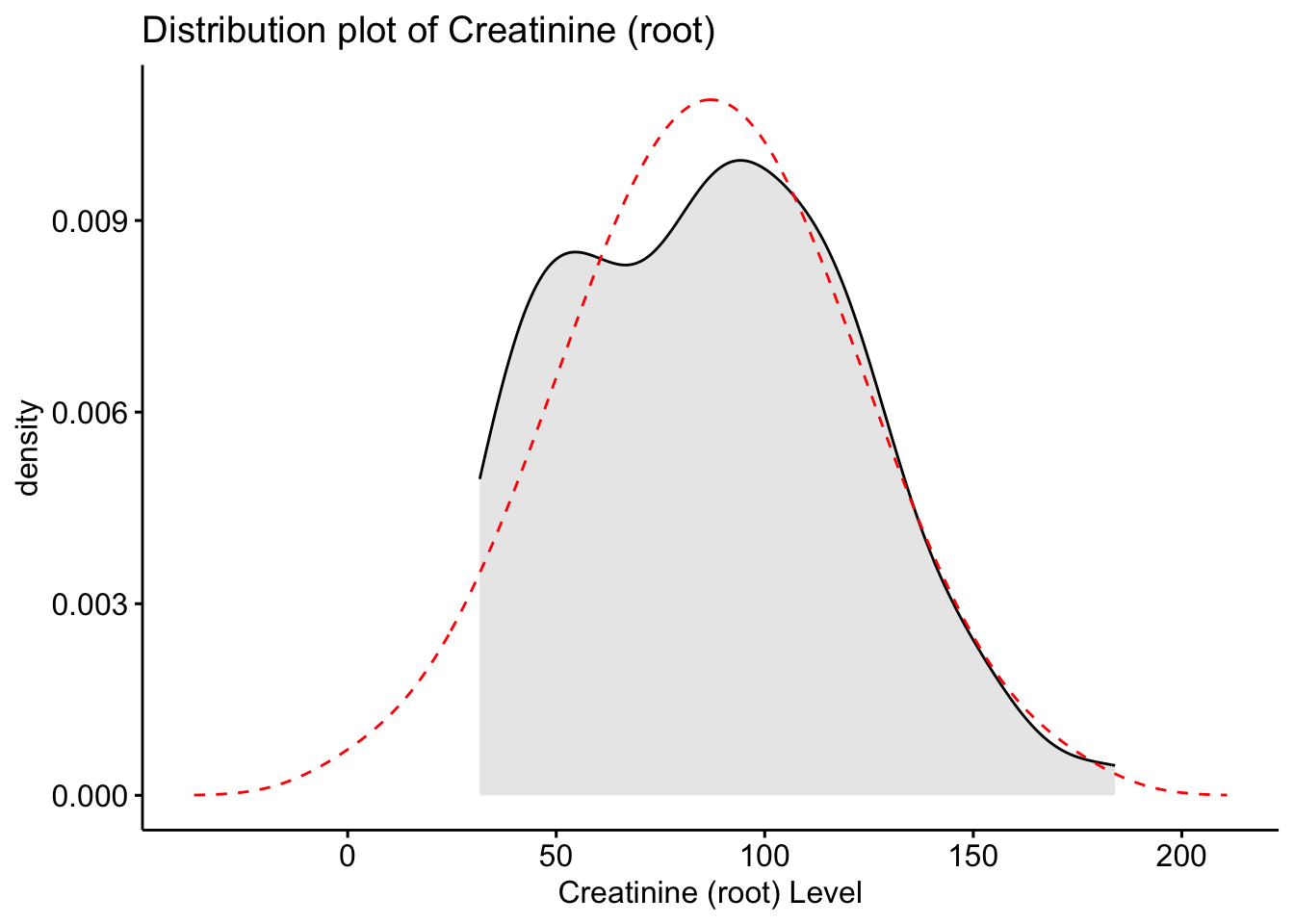

Here we see that the root transformed data is now closer to the normal distribution, however, still is not fully aligned.

Log Transformation

Code

# Transforming the original data into a log transformed variable.
Meta_df$Citrate_log <- log(Meta_df$Citrate)
Meta_df$Creatine_log <- log(Meta_df$Creatine)
Meta_df$Creatinine_log <- log(Meta_df$Creatinine)

# Create a histogram and q-q plot of the newly created log transformed variables.
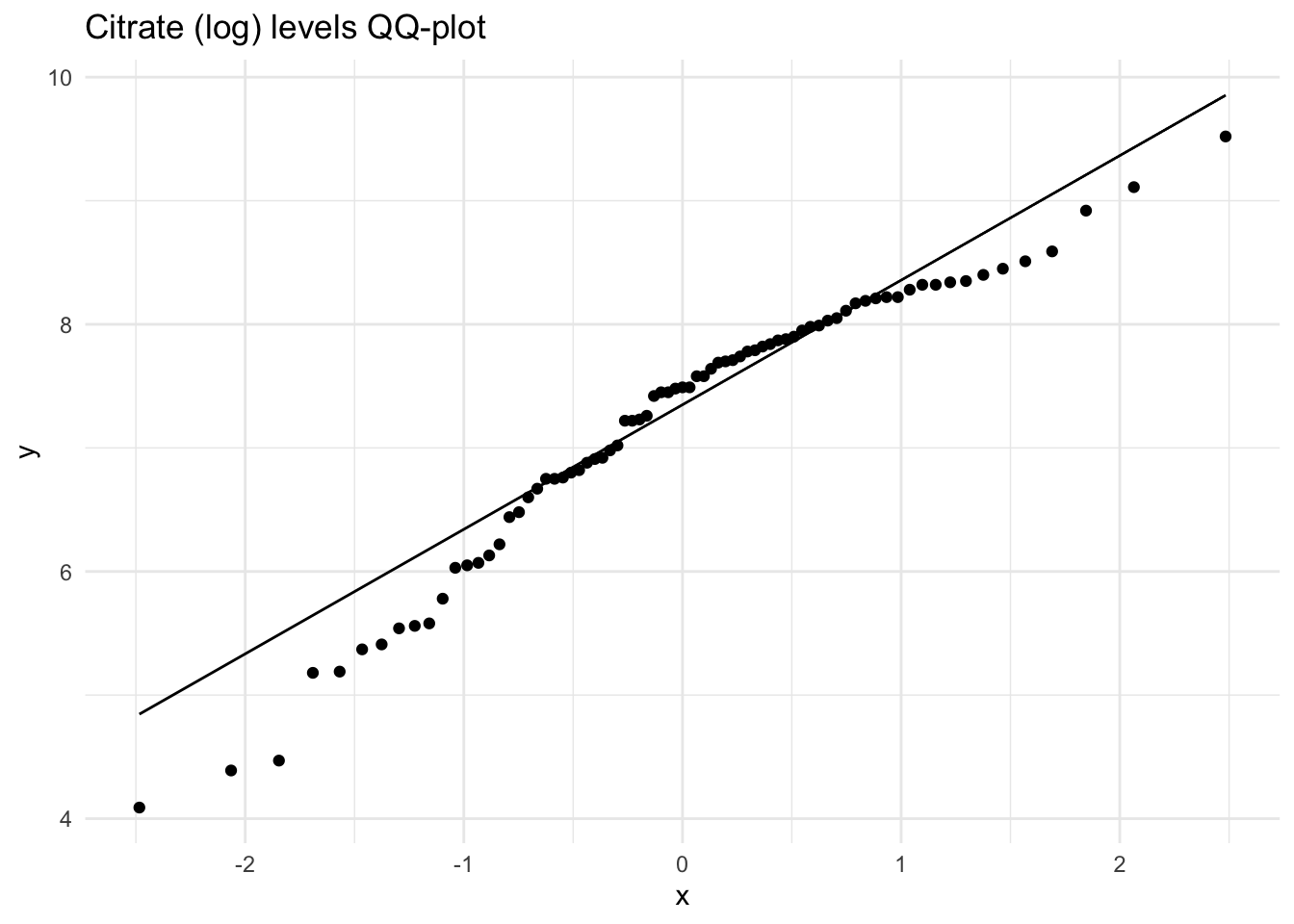
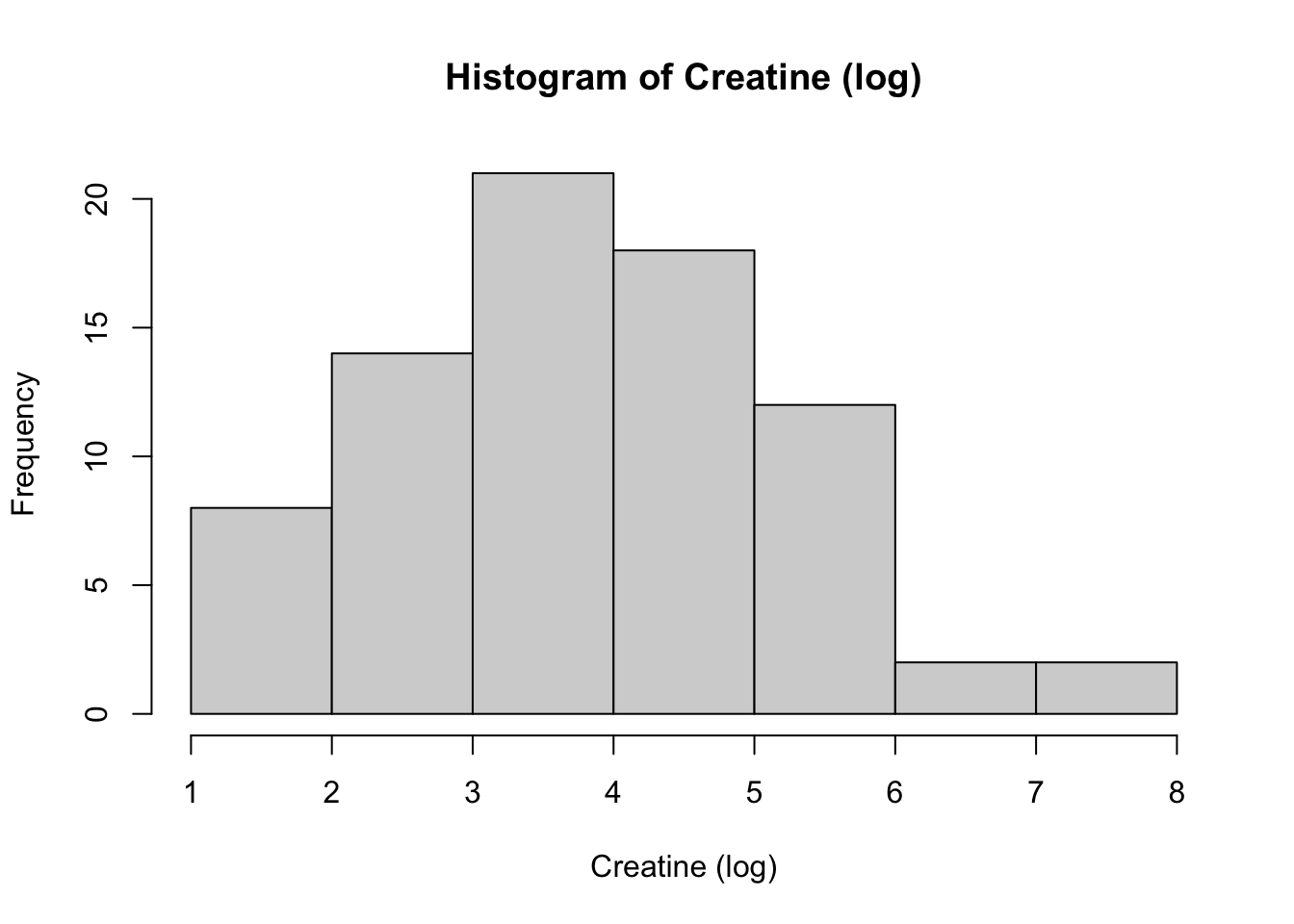
hist(Meta_df$Citrate_log,
     main = "Histogram of Citrate (log)",
     xlab = "Citrate (log)")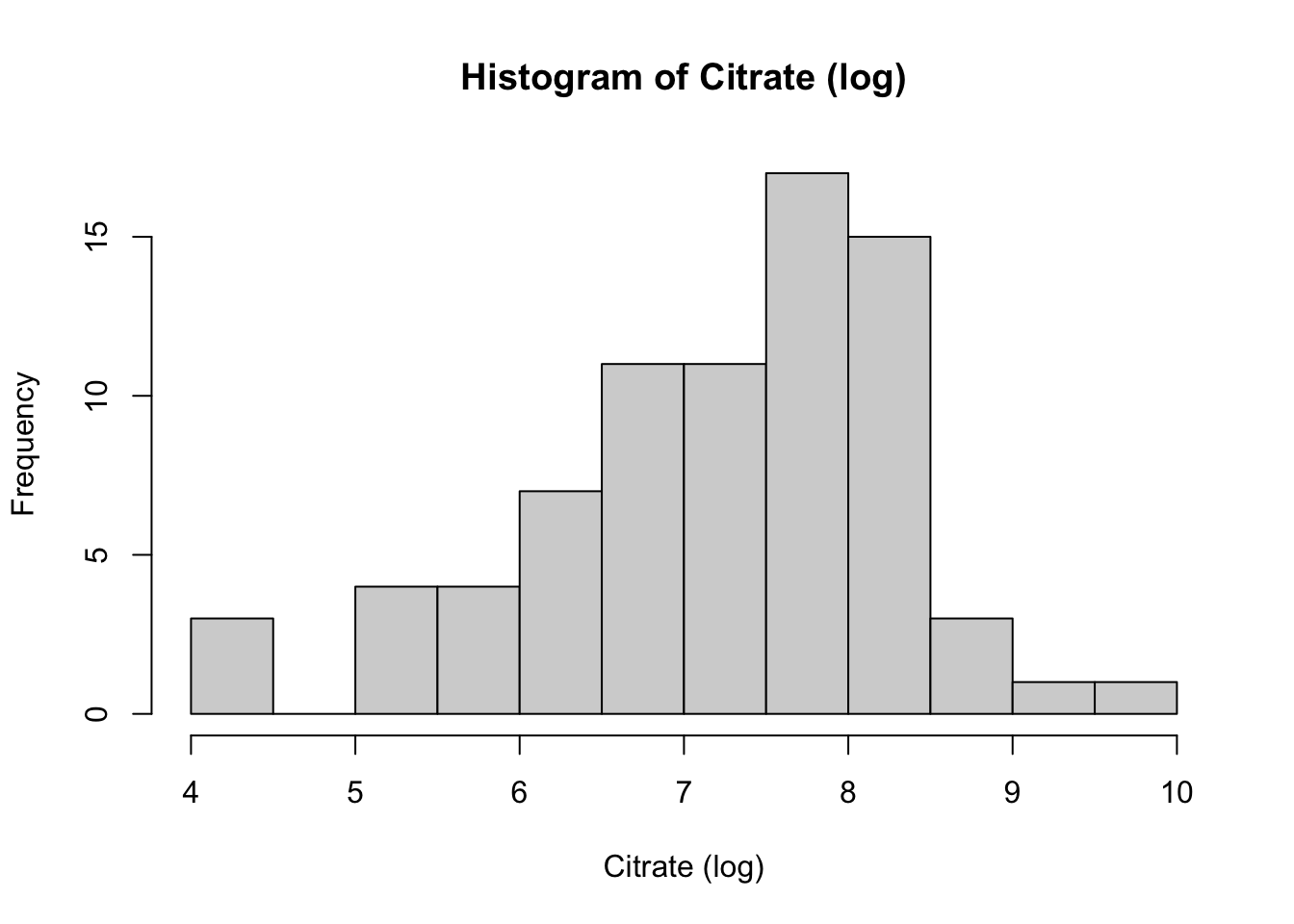

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Citrate_log) +
  labs(title = "Citrate (log) levels QQ-plot") +
  stat_qq() + stat_qq_line()

Code

hist(Meta_df$Creatine_log,
     main = "Histogram of Creatine (log)",
     xlab = "Creatine (log)")

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Creatine_log) +
  labs(title = "Creatine (log) levels QQ-plot") +
  stat_qq() + stat_qq_line()

Code

hist(Meta_df$Creatinine_log,
     main = "Histogram of Creatinine (log)",
     xlab = "Creatinine (log)")

Code

ggplot(data = Meta_df) +
  theme_minimal() +
  aes(sample = Creatinine_log) +
  labs(title = "Creatinine (log) levels QQ-plot") +
  stat_qq() + stat_qq_line()

Code

# Create a plot of the distribution of the new log variable for Citrate.
ggdensity(Meta_df$Citrate_log, fill = "lightgray", title = "Distribution plot of Citrate (log)") +
  scale_x_continuous() +
  xlab("Citrate (log) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Create a plot of the distribution of the new log variable for Creatine.
ggdensity(Meta_df$Creatine_log, fill = "lightgray", title = "Distribution plot of Creatine (log)") +
  scale_x_continuous() +
  xlab("Creatine (log) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

Code

# Create a plot of the distribution of the new log variable for Creatinine.
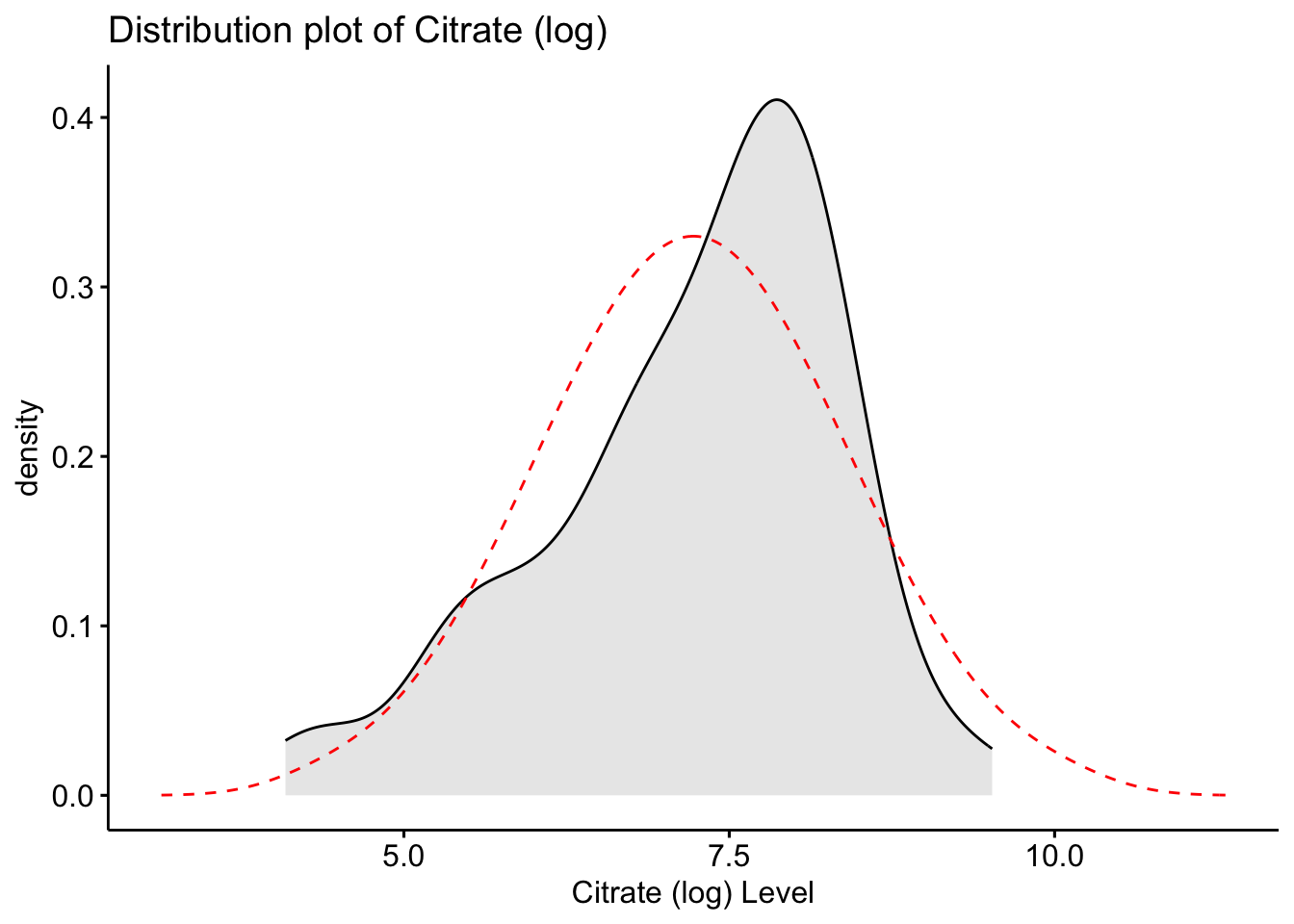
ggdensity(Meta_df$Creatinine_log, fill = "lightgray", title = "Distribution plot of Creatinine (log)") +
  scale_x_continuous() +
  xlab("Creatinine (log) Level") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")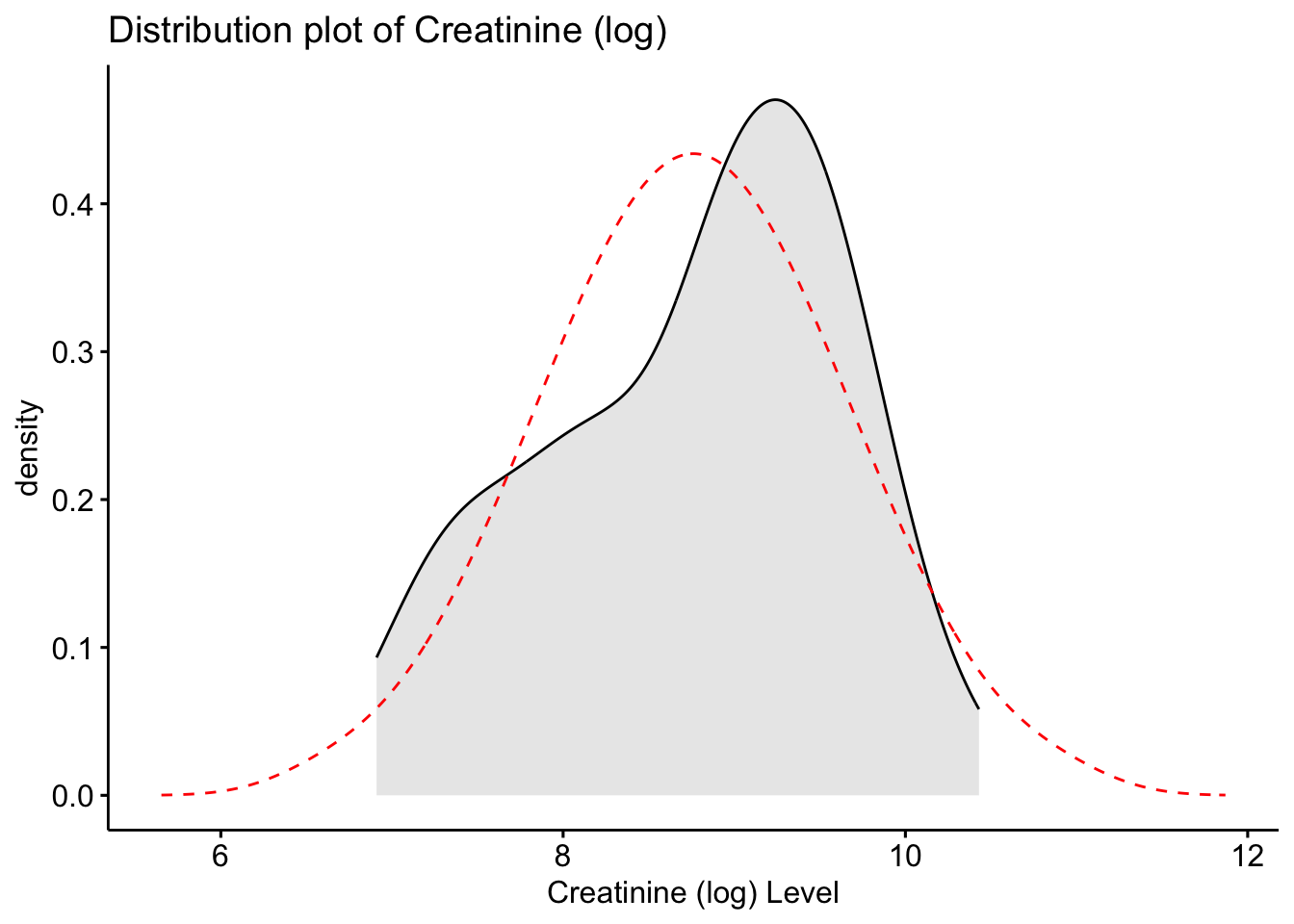

These histograms and plots show that our three variables are now closer to normal distribution, however, two of them might need to be adjusted by using other methods. One thing that can be done is to check the assumptions of normality with these new variables to see if normality has been met. If not, then the data might need to be adjusted accordingly using the other methods of transformation.

Now we will compare the skew and kurtosis values of the new variables.

Code

# Viewing the new skew and kurtosis values for the new rooted and log variables
describe(Meta_df)

                vars  n    mean      sd  median trimmed     mad     min
Patient ID*        1 77   39.00   22.37   39.00   39.00   28.17    1.00
Muscle loss*       2 77    1.39    0.49    1.00    1.37    0.00    1.00
Citrate            3 77 2235.35 2166.57 1790.05 1928.24 1687.32   59.74
Creatine           4 77  126.83  273.22   44.26   71.83   53.88    2.75
Creatinine         5 77 8733.97 6477.62 7631.20 7994.69 6621.16 1002.25
Citrate_root       6 77   42.53   20.78   42.31   41.51   20.27    7.73
Creatine_root      7 77    8.74    7.14    6.65    7.62    4.79    1.66
Creatinine_root    8 77   87.01   34.33   87.36   85.64   41.83   31.66
Citrate_log        9 77    7.22    1.13    7.49    7.31    1.04    4.09
Creatine_log      10 77    3.84    1.41    3.79    3.81    1.45    1.01
Creatinine_log    11 77    8.76    0.86    8.94    8.80    0.93    6.91
                     max    range  skew kurtosis     se
Patient ID*        77.00    76.00  0.00    -1.25   2.55
Muscle loss*        2.00     1.00  0.44    -1.83   0.06
Citrate         13629.61 13569.87  2.43     9.00 246.90
Creatine         1863.11  1860.36  4.84    25.42  31.14
Creatinine      33860.35 32858.10  1.15     1.64 738.19
Citrate_root      116.75   109.02  0.66     0.88   2.37
Creatine_root      43.16    41.51  2.47     8.25   0.81
Creatinine_root   184.01   152.35  0.29    -0.55   3.91
Citrate_log         9.52     5.43 -0.73     0.05   0.13
Creatine_log        7.53     6.52  0.16    -0.42   0.16
Creatinine_log     10.43     3.52 -0.41    -0.84   0.10

As you can see, the new rooted variable values for skew and kurtosis are now much lower and than the original variables, with the log transformed variables being the most preferred and acceptable, though additional transformation or testing might be necessary.

Comparing the `describe() function` to the `skimr() function`

Code

skim(Meta_df)

Data summary
Name	Meta_df
Number of rows	77
Number of columns	11
_______________________
Column type frequency:
character	2
numeric	9
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	empty	n_unique	whitespace
Patient ID	0	1	7	12	0	77	0
Muscle loss	0	1	7	8	0	2	0

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Citrate	1	2235.35	2166.57	59.74	788.40	1790.05	3071.74	13629.61	▇▃▁▁▁
Creatine	1	126.83	273.22	2.75	17.64	44.26	117.92	1863.11	▇▁▁▁▁
Creatinine	1	8733.97	6477.62	1002.25	3498.19	7631.20	12332.58	33860.35	▇▅▂▁▁
Citrate_root	1	42.53	20.78	7.73	28.08	42.31	55.42	116.75	▆▇▆▁▁
Creatine_root	1	8.74	7.14	1.66	4.20	6.65	10.86	43.16	▇▂▁▁▁
Creatinine_root	1	87.01	34.33	31.66	59.15	87.36	111.05	184.01	▇▇▇▃▁
Citrate_log	1	7.22	1.13	4.09	6.67	7.49	8.03	9.52	▁▃▃▇▁
Creatine_log	1	3.84	1.41	1.01	2.87	3.79	4.77	7.53	▃▅▇▃▁
Creatinine_log	1	8.76	0.86	6.91	8.16	8.94	9.42	10.43	▃▃▅▇▂

Shapiro-Wilcox test

Code

shapiro.test(Meta_df$Citrate_log)


    Shapiro-Wilk normality test

data:  Meta_df$Citrate_log
W = 0.9499, p-value = 0.004245

Code

shapiro.test(Meta_df$Creatine_log)


    Shapiro-Wilk normality test

data:  Meta_df$Creatine_log
W = 0.98542, p-value = 0.5266

Code

shapiro.test(Meta_df$Creatinine_log)


    Shapiro-Wilk normality test

data:  Meta_df$Creatinine_log
W = 0.95767, p-value = 0.0118

Conclusion

Here we found three metabolite variables that were right skewed, and we worked through transforming these variables to meet the assumptions of normal distribution. Now that these distributions have been adjusted, we can use them in analyses like ANOVA or Regression models as long as the normal distribution assumption is not violated.

Transforming Data

Introduction

Skewness and Common Transformation

Assumptions

Installing Necessary Packages

Package descriptions

Reading Metabolites Data

Variables of Interest

Check For Normality

Transforming Right Skewed Data

Root Transformation

Log Transformation

Comparing the describe() function to the skimr() function

Shapiro-Wilcox test

Conclusion

Comparing the `describe() function` to the `skimr() function`